1. 누적 합 알고리즘 정의
누적 합 혹은 부분 합 알고리즘은 말 그대로 구하고자 하는 구간의 누적된 합을 구하는 것이다.
예를 들어, 배열의 i ~ j 까지의 합을 구하고자 할 때 하나씩 더해가는 방식을 사용하는 경우에 최악의 경우 O(n^2) 시간복잡도가 생기기 때문에 메모리 낭비 혹은 시간이 오래 걸리는 문제가 발생한다. 이 문제를 해결 하기 위해서는 누적된 합을 구해 필요한 부분만 사용하고, O(N), O(1) 시간까지 단축시킬 수 있다.
2. 1차원 배열
| 인덱스 | 0 | 1 | 2 | 3 | 4 |
| 배열 | 10 | 20 | 30 | 40 | 50 |
| 누적 합 | 10 | 30 | 60 | 100 | 150 |
위 배열에서 인덱스 2번~4번 구간의 합을 구한다고 해보자. 4번 인덱스의 누적 합은 150(0번째~4번째 합)이다. 그러나 우리는 인덱스 2번부터 구해야 하기 때문에 필요없는 구간인 0 ~ 1번째는 빼줘야 한다.
그렇다면 0번과 1번 인덱스의 값을 빼줘야 하나? 아니다. 1번 또한 0번째의 값이 누적이 돼서 계산됐기 때문에 1번 인덱스만 빼주면 된다. 따라서 4번 인덱스에서 1번 인덱스를 빼주면 된다.
배열 i항부터 j항까지의 합을 S(i, j)라고 하면, S(i, j) = prefix_sum[j] - prefix_sum[i - 1]
S[j] - S[i-1] = a[i] + a[i+1] + ... + a[j-1] + a[j]파이썬 코드
array = [10, 20, 30, 40, 50]
n = len(array)
prefix_sum = [0] * (n + 1)
for i in range(n):
prefix_sum[i + 1] = prefix_sum[i] + array[i]
#결과 : prefix_sum[0, 10, 30, 60, 100, 150]
3. 2차원 배열

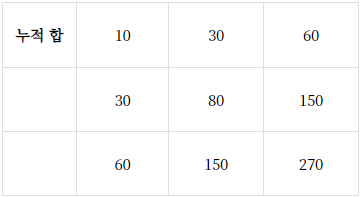
prefix_sum[i][j] = arr[i-1][j-1] + prefix_sum[i-1][j] + prefix_sum[i][j-1] - prefix_sum[i-1][j-1]파이썬 코드
arr = [[10, 20, 30],
[20, 30, 40],
[30, 40, 50]]
m = 3 #열
n = 3 #행
prefix_sum = [[0 for _ in range(m+1)] for _ in range(n+1)]
for i in range(1, n+1):
for j in range(1, m+1):
prefix_sum[i][j] = arr[i - 1][j - 1] + prefix_sum[i - 1][j]
+ prefix_sum[i][j - 1] - prefix_sum[i - 1][j - 1]
for i in range(n+1):
print(prefix_sum[i])
#결과
[0, 0, 0, 0]
[0, 10, 30, 60]
[0, 30, 80, 150]
[0, 60, 150, 270]2차원 배열 참고 - https://yiyj1030.tistory.com/489
[알고리즘] 부분합, 누적합 (Prefix Sum) 쉽게 알아보기(파이썬)
부분합, 누적합이라고 불리우는 배열의 일부 구간에 대한 합을 매우 빠르게 구할 수 있게 해주는 스킬이다. N개의 원소로 이루어진 배열이 주어졌을 때 반복문을 통해 부분 배열의 합을 구하려
yiyj1030.tistory.com
4. 백준 누적 합 문제
1차원
2851번: 슈퍼 마리오
첫째 줄에 마리오가 받는 점수를 출력한다. 만약 100에 가까운 수가 2개라면 (예: 98, 102) 마리오는 큰 값을 선택한다.
www.acmicpc.net
2851번 풀이 : https://dev-cloud.tistory.com/136
11659번: 구간 합 구하기 4
첫째 줄에 수의 개수 N과 합을 구해야 하는 횟수 M이 주어진다. 둘째 줄에는 N개의 수가 주어진다. 수는 1,000보다 작거나 같은 자연수이다. 셋째 줄부터 M개의 줄에는 합을 구해야 하는 구간 i와 j
www.acmicpc.net
11659번 풀이 : https://dev-cloud.tistory.com/137
2차원
2167번: 2차원 배열의 합
첫째 줄에 배열의 크기 N, M(1 ≤ N, M ≤ 300)이 주어진다. 다음 N개의 줄에는 M개의 정수로 배열이 주어진다. 배열에 포함되어 있는 수는 절댓값이 10,000보다 작거나 같은 정수이다. 그 다음 줄에는
www.acmicpc.net
11660번: 구간 합 구하기 5
첫째 줄에 표의 크기 N과 합을 구해야 하는 횟수 M이 주어진다. (1 ≤ N ≤ 1024, 1 ≤ M ≤ 100,000) 둘째 줄부터 N개의 줄에는 표에 채워져 있는 수가 1행부터 차례대로 주어진다. 다음 M개의 줄에는 네
www.acmicpc.net
11660번 풀이 : https://dev-cloud.tistory.com/142
'알고리즘' 카테고리의 다른 글
| [알고리즘] DP (Dynamic Programming, 동적 계획법) (0) | 2023.09.25 |
|---|---|
| [알고리즘] 에라토스테네스의 체 (1) | 2023.09.23 |
| [알고리즘] BFS/DFS 알고리즘 (그래프 탐색) (0) | 2023.05.15 |
| Greedy (그리디 알고리즘) (0) | 2023.05.07 |
| Brute Force (완전 탐색 알고리즘) (0) | 2022.08.05 |