에라토스테네스의 체란?
소수를 찾는 방법으로, 고대 그리스 수학자 에라토스테네스가 발견했다. 이 알고리즘을 사용하지 않고 단순히 소수를 구하려고 할 때 시간이 오래 걸리므로 소수를 구하고자 할 때 에라토스테네스의 체 알고리즘을 사용하는 것이 훨씬 효율적이다.
Alogrithm
- 2부터 소수를 구하고자 하는 구간의 모든 수를 나열한다. 그림에서 회색 사각형으로 두른 수들이 여기에 해당한다.
- 2는 소수이므로 오른쪽에 2를 쓴다. (빨간색으로 표시)
- 자기 자신을 제외한 2의 배수를 모두 지운다. (선홍색으로 표시)
- 남아있는 수 가운데 2의 다음인 3은 소수이므로 오른쪽에 3을 쓴다. (초록색으로 표시)
- 자기 자신을 제외한 3의 배수를 모두 지운다. (연초록으로 표시)
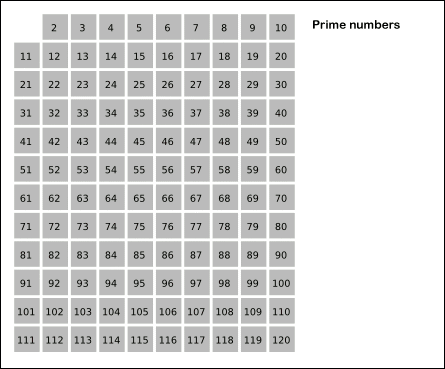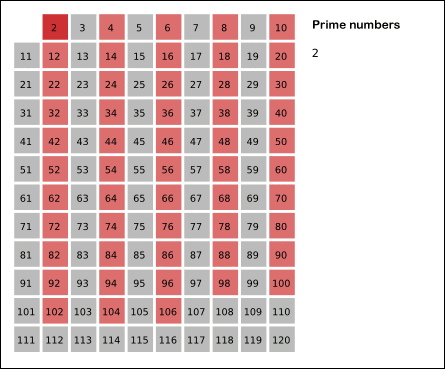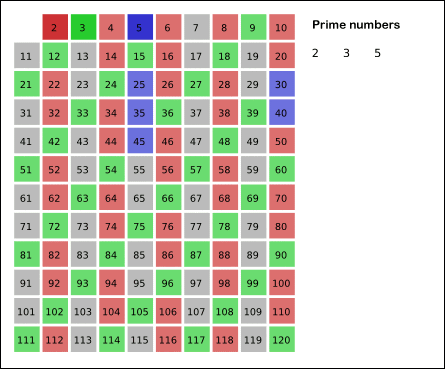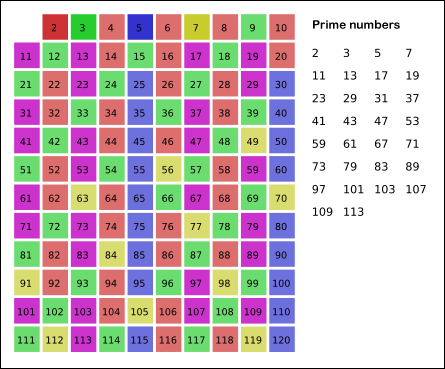
- 위의 과정을 반복하면 구하고자 하는 구간의 모든 소수가 남게 된다.
Python
방법 1 (함수로 정의)
def prime_list(n):
# 에라토스테네스의 체 초기화: n개 요소에 True 설정(소수로 간주)
sieve = [True] * n
# n의 최대 약수가 sqrt(n) 이하이므로 i=sqrt(n)까지 검사
m = int(n ** 0.5)
for i in range(2, m + 1):
if sieve[i] == True: # i가 소수인 경우
for j in range(i+i, n, i): # i이후 i의 배수들을 False 판정
sieve[j] = False
# 소수 목록 산출
return [i for i in range(2, n) if sieve[i] == True]방법 2
n = int(input())
a = [True] * (n + 1)
m = int(n**0.5)
for i in range(2, m + 1):
if a[i] == True:
for j in range(i + i, n + 1, i):
a[j] = False
print([i for i in range(2, n + 1) if a[i] == True])✒ n**0.5 or sqrt(n) 을 하는 이유
sqrt(n) 이하의 숫자만 하면 되는데, 만약 n이 소수이고 n보다 작은 합성수 m = ab라고 하면 a와 b 둘 중 하나는 sqrt(n)보다 무조건 작기 때문이다.
자세한 설명 아래 링크
에라토스테네스의 체 혹은 소수판정 시 제곱근 까지만 확인하면 되는 이유
흔히 에라토스테네스의 체를 사용해 n 이하의 모든 소수를 구하려고 할 때, 효율적으로 구하기 위해 n의 제곱근( sqrt(n) ) 까지만 확인하곤 한다. 1년전쯤엔 n까지 다 확인하거나, 좀 머리 쓴다고 n/
nahwasa.com
C/C++
void Eratos(int n)
{
/* 만일 n이 1보다 작거나 같으면 함수 종료 */
if (n <= 1) return;
/* 2부터 n까지 n-1개를 저장할 수 있는 배열 할당
배열 참조 번호와 소수와 일치하도록 배열의 크기는
n+1 길이만큼 할당(인덱스 번호 0과 1은 사용하지 않음) */
bool* PrimeArray = new bool[n + 1];
/* 배열초기화: 처음엔 모두 소수로 보고 true값을 줌 */
for (int i = 2; i <= n; i++)
PrimeArray[i] = true;
/* 에라토스테네스의 체에 맞게 소수를 구함
만일, PrimeArray[i]가 true이면 i 이후의 i 배수는 약수로 i를
가지고 있는 것이 되므로 i 이후의 i 배수에 대해 false값을 준다.
PrimeArray[i]가 false이면 i는 이미 소수가 아니므로 i의 배수 역시
소수가 아니게 된다. 그러므로 검사할 필요도 없다.
또한 i*k (k < i) 까지는 이미 검사되었으므로 j시작 값은 i*2에서 i*i로 개선할 수 있다.
*/
for (int i = 2; i * i <= n; i++)
{
if (PrimeArray[i])
for (int j = i * i; j <= n; j += i)
PrimeArray[j] = false;
}
// 이후의 작업 ...
}JAVA
import java.util.*;
class Main {
public static int n = 1000; // 2부터 1,000까지의 모든 수에 대하여 소수 판별
public static boolean[] arr = new boolean[n + 1];
public static void main(String[] args) {
Arrays.fill(arr, true); // 처음엔 모든 수가 소수(True)인 것으로 초기화(0과 1은 제외)
// 에라토스테네스의 체 알고리즘 수행
// 2부터 n의 제곱근까지의 모든 수를 확인하며
for (int i = 2; i <= Math.sqrt(n); i++) {
// i가 소수인 경우(남은 수인 경우)
if (arr[i] == true) {
// i를 제외한 i의 모든 배수를 지우기
int j = 2;
while (i * j <= n) {
arr[i * j] = false;
j += 1;
}
}
}
// 모든 소수 출력
for (int i = 2; i <= n; i++) {
if (arr[i]) System.out.print(i + " ");
}
}
}'알고리즘' 카테고리의 다른 글
| [자료구조] sort, sorted, 정렬, 이중 리스트 정렬 (Python) (0) | 2023.10.31 |
|---|---|
| [알고리즘] DP (Dynamic Programming, 동적 계획법) (0) | 2023.09.25 |
| [알고리즘] BFS/DFS 알고리즘 (그래프 탐색) (0) | 2023.05.15 |
| Greedy (그리디 알고리즘) (0) | 2023.05.07 |
| 누적 합(Prefix Sum, 부분 합) (0) | 2023.03.27 |